
大模型RAG技術:從入門到實踐
拓撲空間的另一種常見定義是通過開集(open sets)。在這種定義中,一個拓撲空間由一個二元組 $(X, au)$ 構成,其中 $X$ 是非空集合,$ au$ 是 $X$ 的子集的集合,且滿足如下性質:
通過開集的定義,我們可以更直觀地理解拓撲空間的結構。
拓撲空間中的鄰域是指包含某個點的一個開集。根據定義,拓撲空間中的鄰域具有以下特性:
這些性質幫助我們理解拓撲空間中點與鄰域之間的關系。
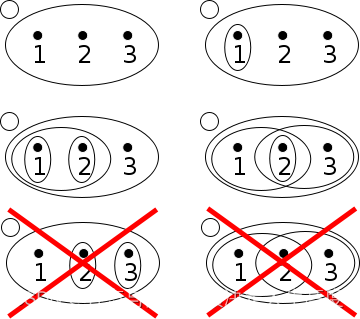
在數學中,我們常常通過集合構造拓撲。例如,假設 $X = {1, 2, 3}$,我們可以構造出不同的拓撲,如:
每個拓撲都滿足基本的拓撲公理,但其結構可能大不相同。
拓撲空間在數學的多個領域中扮演著重要角色。它不僅是分析學、幾何學的重要工具,還涉及到代數拓撲和微分拓撲等領域。在這些領域中,拓撲空間幫助我們研究空間的連續性和變換。
物理學中,拓撲空間常用于研究宇宙的結構和物質的性質。例如,在量子場論中,拓撲空間幫助我們理解粒子的相互作用和對稱性。
拓撲空間的概念也被引入到計算機科學中,特別是在數據分析和機器學習領域。在這些領域中,拓撲空間用于處理數據的幾何結構和高維數據的映射。
考慮集合 $X = {a, b, c}$,我們可以定義一個拓撲 $tau = {emptyset, X, {a, b}, {b, c}}$。此拓撲滿足所有拓撲公理:
假設我們有一個集合 $Y = {1, 2, 3, 4}$,定義拓撲為 $sigma = {emptyset, Y, {1, 2}, {3, 4}}$。這是一個合法的拓撲,因為:
問:什么是拓撲空間的基本要素?
問:拓撲空間如何應用于計算機科學?
問:拓撲空間與向量空間有何區別?
問:如何通過例子理解拓撲空間?
問:拓撲空間在物理學中有何應用?
通過本文的探討,我們了解了拓撲空間的基本概念、特性以及其在數學、物理和計算機科學中的廣泛應用。拓撲空間不僅是一個數學定義,更是理解復雜系統和結構的重要工具。