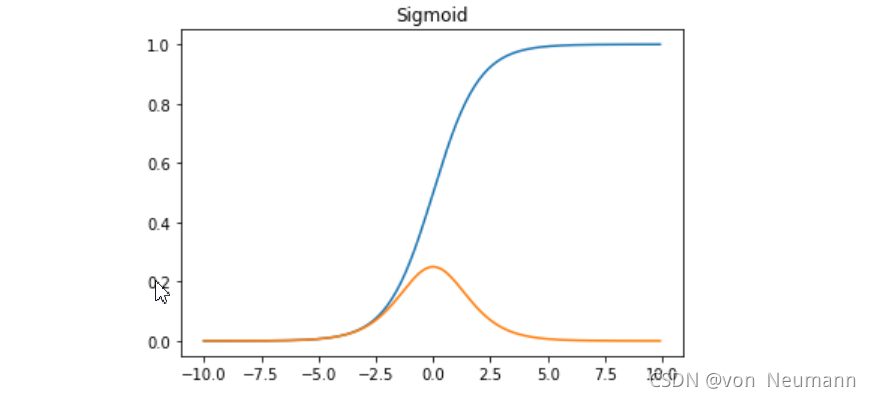
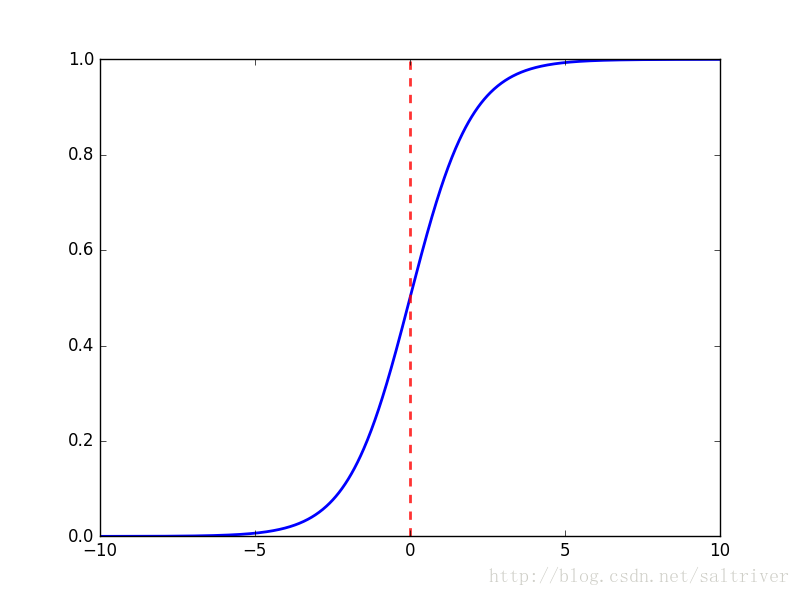
Sigmoid函數(shù)連續(xù)、光滑、嚴(yán)格單調(diào),以(0,0.5)為中心對(duì)稱,是一個(gè)非常良好的閾值函數(shù)。
Sigmoid函數(shù)的值域限制在(0,1)之間,這與概率值的范圍相對(duì)應(yīng),使得Sigmoid函數(shù)能夠與概率分布聯(lián)系起來。
邏輯回歸(LR)模型是一個(gè)二分類模型,它通過Sigmoid函數(shù)將線性組合的特征映射到概率空間。Sigmoid函數(shù)在此扮演了將線性模型的輸出轉(zhuǎn)換為概率預(yù)測的關(guān)鍵角色。
Sigmoid函數(shù)的導(dǎo)數(shù)是其本身的函數(shù),即:
f'(x) = f(x) * (1 - f(x))這種性質(zhì)使得在優(yōu)化過程中計(jì)算梯度變得非常方便,節(jié)省了計(jì)算時(shí)間。
Sigmoid函數(shù)的輸出可以直接解釋為概率,這為模型的解釋性和結(jié)果的理解提供了極大的便利。
Sigmoid函數(shù)因其數(shù)學(xué)上的處理便利性和推導(dǎo)特性,成為邏輯回歸模型的首選。它不僅滿足LR模型對(duì)函數(shù)的兩個(gè)基本要求——取值范圍在0~1之間,且在0.5處中心對(duì)稱——還因其單調(diào)性和可微性,成為連接線性模型和概率預(yù)測的理想選擇。
正態(tài)分布解釋和最大熵解釋提供了Sigmoid函數(shù)選擇的另一種視角。正態(tài)分布因其普遍性,在未知概率分布形式時(shí)成為首選。Sigmoid函數(shù)因其與正態(tài)分布積分形式的相似性,成為計(jì)算上更優(yōu)的替代。最大熵解釋則從信息論的角度,解釋了在給定假設(shè)下,為何Sigmoid函數(shù)能夠提供最均勻的分布。

通過圖像,我們可以直觀地看到Sigmoid函數(shù)的形狀及其導(dǎo)數(shù)的變化,這有助于我們更好地理解其在模型中的應(yīng)用和影響。
通過上述分析,我們可以看到Sigmoid函數(shù)在機(jī)器學(xué)習(xí)中的重要性和應(yīng)用。雖然它有其局限性,但在適當(dāng)?shù)膱鼍跋拢琒igmoid函數(shù)仍然是一個(gè)強(qiáng)大的工具。