
數據庫表關聯:構建高效數據結構的關鍵
這表明隨機事件A在$n$次試驗中發生的頻率會以概率收斂于$p$。隨著實驗次數的增加,事件發生的頻率會無限接近于事件的概率。

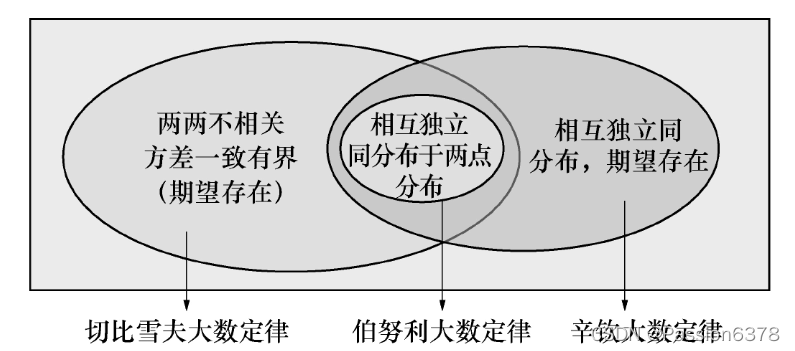
辛欽大數定律適用于更廣泛的情形,即隨機變量獨立同分布且具有相同的數學期望$mu$。對于$n$個獨立同分布的隨機變量$X_1, X_2,…X_n$,有:
$$
limlimits_{ntoinfty} Pleft(left|frac{Sigma_1^nX_k}{n}-muright|< epsilonright) = 1
$$
這表明,隨著觀察次數的增加,樣本平均值將趨近于期望值。這是用算術平均值計算期望的理論基礎。

切比雪夫大數定律適用于方差有限的隨機變量序列。設隨機變量序列$X_1, X_2,…X_n$,它們兩兩不相關,且方差存在并有共同上界,則:
$$
limlimits_{ntoinfty} Pleft(left|frac{Sigma_1^nX_k-Sigma_1^nmu_k}{n}right|< epsilonright) = 1
$$
這個定理不要求隨機變量同分布,但對方差有較高的要求。它通過樣本平均數估計總體平均數提供了理論支持。

中心極限定理則探討了獨立同分布隨機變量序列的標準化和正態分布的關系。假設隨機變量序列$X_1, X_2,…X_n$獨立同分布,且期望$
mu$和方差$sigma^2$存在,那么:
$$
limlimits_{ntoinfty} Pleft(frac{Sigma_1^nX_k-nmu}{sqrt{n}sigma}le xright) = Phi(x)
$$
其中$Phi(x)$為標準正態分布函數。這意味著無論原始分布如何,足夠多的獨立同分布變量的和經過適當標準化后會趨向正態分布。
在統計學中,大數定理提供了抽樣理論的基礎。它幫助我們理解樣本平均如何反映總體平均,并在金融、物理、社會科學等領域廣泛應用。例如,在金融市場中,投資者利用大數定理來分析股票回報的長期平均趨勢。
通過一個簡單的骰子擲投實驗,我們可以直觀理解大數定理。假設我們連續投擲一個均勻的六面骰子,期望值為3.5。根據大數定理,隨著投擲次數的增加,平均值應趨近于3.5。
clear all;
clf;
clc;
num_trials = 1000;
trials = randi(6, [1 num_trials]);
figure(1);
plot(cumsum(trials)./(1:num_trials), 'r-');
hold on;
plot([1 num_trials], [3.5 3.5], 'color', [0 0.5 0]);
title('average dice value against number of rolls');
xlabel('trials');
ylabel('mean value');
legend('average', 'y=3.5');
axis([0 num_trials 1 6]);
弱大數定理是辛欽大數定律的一種形式,適用于獨立同分布的隨機變量,具有數學期望$E(X_k)=mu$。在$n$個隨機變量的算術平均中:
$$
limlimits{ntoinfty} Pleft(left|frac{1}{n}Sigma{k=1}^{n}X_k-muright|<epsilonright)=1
$$
這表明,當樣本數量足夠多時,樣本均值接近真實均值的概率趨于1。
概率收斂是大數定理中的一個重要概念,它表示隨著試驗次數增加,樣本統計量趨近于理論值的概率增加。通過實際操作,如反復擲骰子,我們可以觀察到這種收斂性。
在物理學中,大數定理也有重要的應用。例如,在熱力學中,通過大量分子運動的統計分析,可以預測氣體的宏觀行為。
大數定理和中心極限定理在統計學中相輔相成,前者關注樣本平均的收斂性,而后者則研究樣本分布的形態變化。二者結合,為統計推斷提供了理論基礎。
大數定理不僅是概率論的一個基本定理,同時也是統計學的基石。無論是在理論研究還是實際應用中,大數定理都扮演著重要角色。它幫助我們理解隨機現象中的確定性規律,并在抽樣、數據分析等方面提供重要指導。
問:大數定理在實際生活中有哪些應用?
問:伯努利大數定律與辛欽大數定律的區別是什么?
問:中心極限定理如何與大數定理關聯?