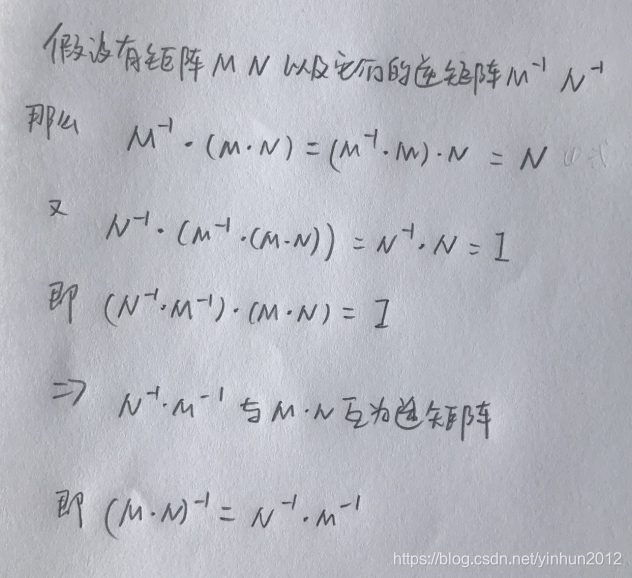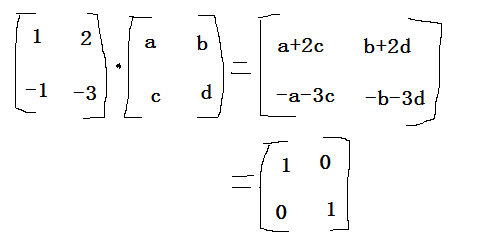
假設(shè)逆矩陣 ( A^{-1} ) 為:
a, b
c, d根據(jù)矩陣乘法的定義,我們可以得到以下方程組:
a + 2c = 1
b + 2d = 0
-a - 3c = 0
-b - 3d = 1解得 ( a = 3 ), ( b = 2 ), ( c = -1 ), ( d = -1 )。
此方法適用于小型矩陣的手動(dòng)計(jì)算,可以有效地幫助理解逆矩陣的求解過程。
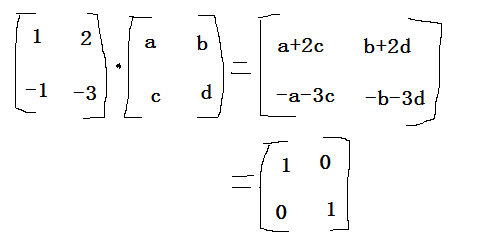
伴隨矩陣法是一種利用矩陣的伴隨矩陣和行列式來求逆矩陣的方法。通過計(jì)算伴隨矩陣,再除以行列式,便可以得到逆矩陣。
設(shè)矩陣 ( A ) 為:
1, 2
-1, -3其伴隨矩陣 ( A^* ) 為:
-3, -2
1, 1行列式 ( |A| ) 為:
1*(-3) - (-1)*2 = -1因此,逆矩陣 ( A^{-1} = frac{A^}{|A|} = -A^ ) 為:
3, 2
-1, -1此方法適用于較小且計(jì)算復(fù)雜度不高的矩陣,尤其是在確定行列式不為零時(shí)。
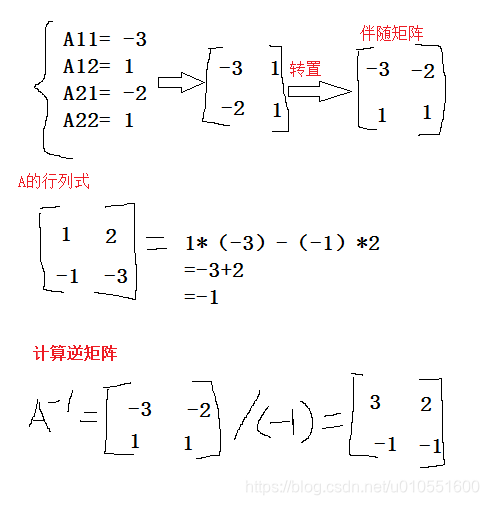
初等變換法通過將矩陣轉(zhuǎn)換為單位矩陣,同時(shí)對(duì)單位矩陣進(jìn)行相同的初等變換,從而得到逆矩陣。
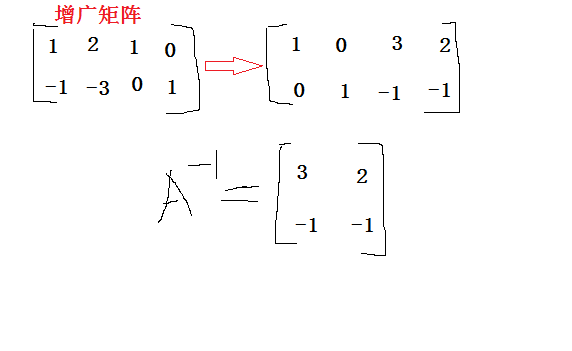
首先寫出增廣矩陣 ( A|I ) :
1 2 1 0
-1 -3 0 1然后進(jìn)行一系列初等行變換:
1 2 1 0
0 -1 1 11 0 3 2
0 -1 1 11 0 3 2
0 1 -1 -1此方法適用于通過一系列行操作求逆的情況,特別是在進(jìn)行矩陣變換時(shí)。
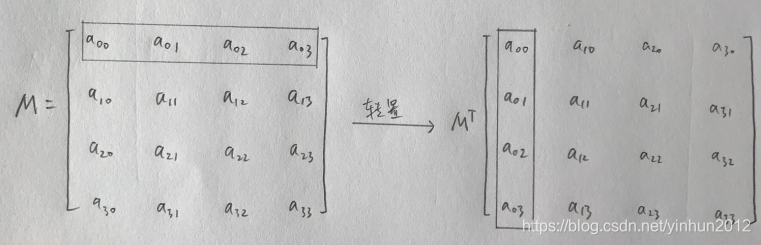
轉(zhuǎn)置矩陣是通過將矩陣的行和列互換得到的新矩陣。對(duì)于矩陣 ( A ) 的轉(zhuǎn)置,記為 ( A^T )。
轉(zhuǎn)置矩陣的行列式值不變。以下是其運(yùn)算性質(zhì):
轉(zhuǎn)置矩陣在矩陣運(yùn)算中經(jīng)常被使用,尤其是在線性代數(shù)和幾何變換中。
逆矩陣是指矩陣 ( A ) 存在一個(gè)矩陣 ( A^{-1} ),使得 ( A times A^{-1} = I ),其中 ( I ) 為單位矩陣。
逆矩陣常用于求解線性方程組、矩陣變換中的逆變換以及圖形學(xué)中的幾何變換。
在三維圖形學(xué)中,逆矩陣用于將變換后的坐標(biāo)還原到原始坐標(biāo)。
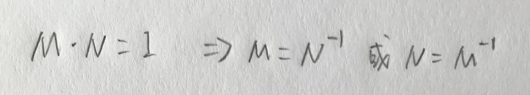
逆矩陣具有多種運(yùn)算性質(zhì),使得復(fù)雜的矩陣運(yùn)算得以簡(jiǎn)化和統(tǒng)一。
這些性質(zhì)在矩陣的組合運(yùn)算、變換和求解中具有重要作用。
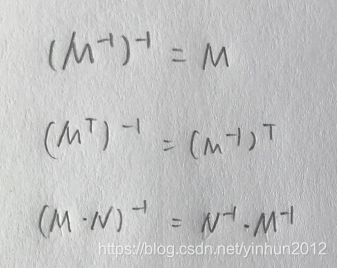
在三維圖形學(xué)中,矩陣逆運(yùn)算用于變換坐標(biāo)系、計(jì)算光影效果等。
通過逆矩陣,可以將物體從世界坐標(biāo)系轉(zhuǎn)換回局部坐標(biāo)系,實(shí)現(xiàn)物體的旋轉(zhuǎn)、縮放和移動(dòng)的逆變換。
在著色器編程中,逆矩陣用于計(jì)算光源位置和觀察位置的變換。