
全網最詳細的Spring入門教程
對數函數是通過對數的定義而形成的一個函數。在數學表達式中,函數 y = log_a(x) 被稱為對數函數,其中 x 是自變量。對數函數的定義域是 x > 0。

對數運算法則是一種特殊的運算方法,用于處理積、商、冪、方根的運算。通過指數和對數的相互轉化,我們可以得到以下運算規則:
兩個正數的積的對數,等于這兩個數的對數的和:
log_a(MN) = log_a(M) + log_a(N)

兩個正數商的對數,等于被除數的對數減去除數對數的差:
log_a(M/N) = log_a(M) – log_a(N)

一個正數冪的對數,等于冪的底數的對數乘以冪的指數:
log_a(M^n) = n * log_a(M)

一個正數的算術根的對數,等于被開方數的對數除以根指數:
log_a(√M) = (1/2) * log_a(M)

在數學中,一個重要的對數恒等式是 a^log_a(N) = N。這一公式的推導如下:
設 log_a(N) = t,那么根據對數的定義,我們有 a^t = N。因此,a^log_a(N) = a^t = N。由此證明了該恒等式的正確性。
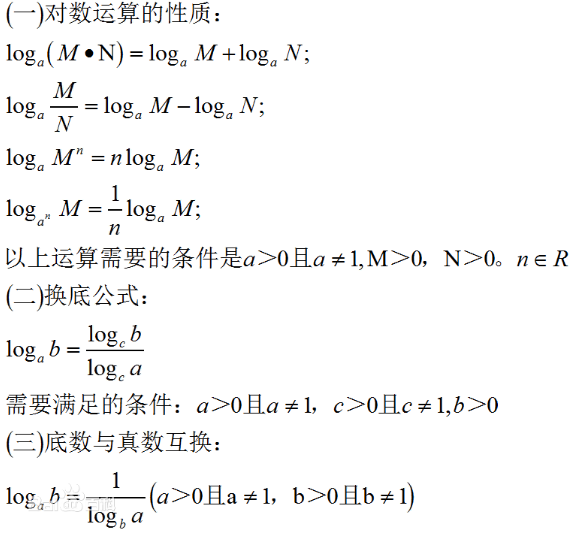
自然對數的底數 e 是一個重要的數學常數,約為 2.71828。其在自然現象中的應用非常廣泛,例如在細胞分裂的模型中,e 描述了在單位時間內持續的增長可以達到的極限。
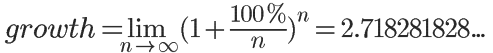
在編程中,對數函數被廣泛應用于算法的復雜度分析、數據的對數變換等場景。例如,Python 中的 math 庫提供了對數函數,可以用于計算對數。
import math
print(math.log(10)) # 輸出為 2.302585092994046
print(math.log10(10)) # 輸出為 1.0對數函數在數學和實際應用中都扮演著重要的角色。通過了解對數的基本定義、性質和運算法則,我們可以更好地應用對數來解決復雜的數學問題和實際工程問題。
問:對數函數的定義域是什么?
問:自然對數的底數 e 有什么實際意義?
問:在編程中如何使用對數函數?