
Node.js 后端開發指南:搭建、優化與部署
反函數的性質是理解和應用反函數的關鍵。以下是一些基本性質:
f(x)與它的反函數f^(-1)(x)圖像關于直線y=x對稱。x=f(y)在開區間I上嚴格單調,可導,且f'(y)≠0,那么它的反函數y=f^(-1)(x)在區間S={x|x=f(y),y∈I}內也可導,且滿足特定的導數關系。y=x的反函數是它本身。在實際應用中,計算反函數通常涉及到解方程。給定一個函數y=f(x),要找到它的反函數,我們需要解出x關于y的表達式,即x=g(y)。這個過程可能涉及到代數變換、因式分解、使用求根公式等數學技巧。
反函數在科學和工程領域有著廣泛的應用。例如,在物理學中,力和加速度的關系可以通過反函數來表達;在化學中,反應速率常數與反應物濃度的關系也可以用反函數來描述。
在編程語言中,反函數的概念也被廣泛應用。例如,在數據庫查詢中,通過反函數可以快速從查詢結果中恢復原始數據。
繪制反函數圖像是理解反函數特性的一個重要手段。通過繪制原函數和反函數的圖像,我們可以直觀地看到它們關于直線y=x的對稱性。
繪制反函數圖像的步驟通常包括:確定原函數的圖像,然后找到關于直線y=x的對稱點,最后連接這些點形成反函數的圖像。
可以使用各種數學軟件和編程語言來繪制反函數圖像,例如MATLAB、Python的matplotlib庫等。
import matplotlib.pyplot as plt
import numpy as np
def f(x):
return x**2
def f_inverse(x):
return np.sqrt(x)
x = np.linspace(-2, 2, 400)
y = f(x)
x_inverse = np.linspace(0, 4, 400)
y_inverse = f_inverse(x_inverse)
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='f(x) = x^2')
plt.plot(x_inverse, y_inverse, label='f^(-1)(x) = sqrt(x)')
plt.plot(np.linspace(-2, 4, 10), np.linspace(-2, 4, 10), 'k--', label='y=x')
plt.legend()
plt.show()通過上述代碼塊,我們可以得到原函數f(x) = x^2和它的反函數f^(-1)(x) = sqrt(x)的圖像,并觀察到它們關于直線y=x的對稱性。
反函數的導數是微積分中的一個重要話題。如果函數f在某個區間上嚴格單調且可導,那么它的反函數在相應的區間上也可以導,并且它們的導數之間存在特定的關系。
如果x=f(y)在開區間I上嚴格單調,可導,且f'(y)≠0,那么它的反函數y=f^(-1)(x)在區間S={x|x=f(y),y∈I}內也可導,且滿足以下關系式:
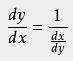
反函數的導數可以從幾何上解釋為曲線在該點處的切線的斜率的倒數。這意味著,如果原函數在某個點處的切線斜率較大,那么它的反函數在對應點處的切線斜率就較小。
考慮函數f(x) = x^3,我們要找到它的反函數的導數。首先,我們找到反函數f^(-1)(x) = x^(1/3),然后計算其導數。
f^(-1)'(x) = (x^(1/3))' = 1/3 * x^(-2/3)答:反函數是一個函數,它能夠將原函數的輸出值映射回輸入值,即如果y=f(x),則x=f^(-1)(y)。
答:一個函數有反函數當且僅當它是一一對應的,即定義域中的每個輸入都有唯一的輸出,反之亦然。
答:反函數的圖像與原函數的圖像關于直線y=x對稱。
答:反函數在科學、工程和編程中有廣泛應用,例如在物理學中描述力和加速度的關系,在數據庫查詢中恢復原始數據等。
答:如果x=f(y)在某個區間上嚴格單調且可導,那么它的反函數y=f^(-1)(x)在相應的區間上也可導,并且它們的導數之間存在特定的關系。