欧美毛片免费网站在线观看,成年网址网站在线观看,久久国产欧美日韩精品免费

2. 梯度下降法的變種

2.1 批量梯度下降法（BGD）

批量梯度下降法使用整個訓練數據集來計算梯度，因此每次迭代的計算開銷較大，但其優點是每次更新方向較為準確。適用于數據集較小的情況。

2.2 隨機梯度下降法（SGD）

隨機梯度下降法每次僅使用一個樣本來計算梯度，因此計算速度較快，適合大規模數據集。其缺點是收斂過程中可能會出現較大波動。

2.3 小批量梯度下降法（MBGD）

小批量梯度下降法結合了批量和隨機梯度下降法的優點，同時使用多個樣本來計算梯度，既提高了計算效率，又減少了波動。

3. 梯度下降法的優缺點

3.1 優點

簡單易實現，適用于多種問題。
能夠處理大規模數據集。
適用于非凸優化問題。

3.2 缺點

可能陷入局部最優解。
需要調整學習率，學習率過大或過小都會影響收斂速度。
對初始值敏感，選擇不當可能導致收斂困難。

4. 梯度下降法在機器學習中的應用

梯度下降法在機器學習中有廣泛的應用，包括線性回歸、邏輯回歸和神經網絡的訓練。

4.1 在線性回歸中的應用

線性回歸模型通過最小化損失函數來擬合數據。梯度下降法通過調整模型參數，使得損失函數達到最小值，從而找到最佳擬合。

import numpy as np

X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3

theta = np.zeros(2)
learning_rate = 0.01

for _ in range(1000):
    gradient = X.T.dot(X.dot(theta) - y) / len(y)
    theta -= learning_rate * gradient

print(f"Optimal parameters: {theta}")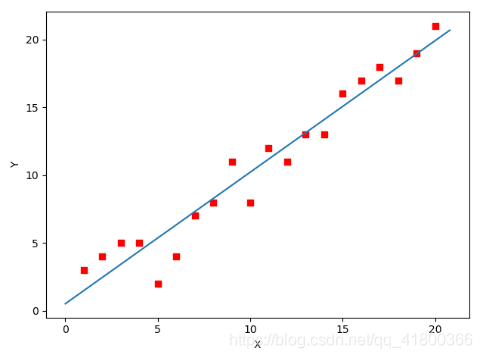

4.2 在邏輯回歸中的應用

邏輯回歸用于二分類問題，通過最大化似然函數來估計模型參數。梯度下降法通過最小化負對數似然函數實現參數估計。

4.3 在神經網絡中的應用

神經網絡通過反向傳播算法進行訓練，梯度下降法用于更新網絡中的權重和偏置。

5. 梯度下降法的調優

調優是提高梯度下降法性能的重要步驟，主要包括學習率的選擇和特征歸一化。

5.1 學習率的選擇

學習率決定了每次迭代的步伐，過大可能導致震蕩，過小則收斂緩慢。常用的方法是使用自適應學習率算法，如AdaGrad、RMSProp等。

5.2 特征歸一化

特征歸一化可以加快收斂速度，常用的方法有標準化和歸一化。

6. 代碼實現

以下是一個使用Python實現梯度下降法的示例代碼。

import numpy as np

theta = np.array([0.0, 0.0])
learning_rate = 0.01

X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3

for _ in range(1000):
    gradient = np.dot(X.T, np.dot(X, theta) - y) / len(y)
    theta -= learning_rate * gradient

print(f"Optimal parameters: {theta}")