
如何高效爬取全球新聞網站 – 整合Scrapy、Selenium與Mediastack API實現自動化新聞采集
在幾何上,向量不僅僅是一個點到另一個點的距離,而是一個從起點到終點的方向和距離的組合。其大小(或長度)稱為模,方向則由線段的方向決定。
向量的模是指向量的長度,用于描述向量的大小。模的計算方式為向量各分量平方和的平方根。例如,一個向量 a = ((x_1, x_2)),其模為 (sqrt{x_1^2 + x_2^2})。
單位向量是模為1的向量,用于表示方向而不考慮大小。通過將一個非零向量除以其模,可以得到對應的單位向量。單位向量在直角坐標系中的例子:
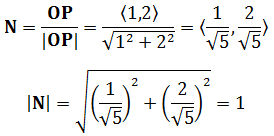
零向量是所有分量均為零的向量,表示沒有方向和大小。它在向量加法中起著類似于數字零在數值加法中的作用。
向量的運算包括加法、減法和數乘,這些運算是線性代數的基礎。
向量加法遵循平行四邊形法則,即兩個向量的和是由起點到兩個向量終點構成的平行四邊形的對角線。具體表示為:
overrightarrow{a} + overrightarrow{b} = (a_1 + b_1, a_2 + b_2)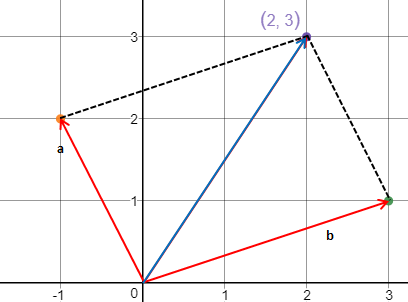
向量數乘是將向量的每個分量乘以一個標量,這會改變向量的大小而不改變方向(若標量為正)。若標量為負,則反向。
向量的減法可視作加上一個負向量,即 (overrightarrow{a} – overrightarrow{b} = overrightarrow{a} + (-overrightarrow{b}))。
在直角坐標系中,向量可以用來描述空間中的位置和方向。通過將向量的起點選為坐標系原點,便可以直觀地表示向量。

向量可以用于解線性方程組,方程組的解可以看作是向量的線性組合。如下為示例方程組的向量表示:
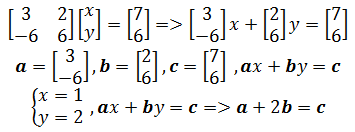
在幾何上,這種表示可以幫助我們理解方程組解的性質和幾何結構。
在物理學中,向量用于描述速度、力等具有方向和大小的物理量。通過向量,我們可以簡化許多復雜的物理問題并進行分析。
力是物理學中常見的向量之一,多個力的合成便是向量加法的直接應用,而力的分解則是將一個力分解為多個方向上的分量。

速度和加速度同樣是向量,描述物體運動的方向和速率的變化。通過向量的加減法,我們能方便地處理運動中的疊加問題。
在編程語言中,向量運算被廣泛應用于計算機圖形學、機器學習和數據分析中。通過一些簡單的代碼示例,我們可以直觀地了解向量運算在程序中的實現。
import numpy as np
a = np.array([1, 2])
b = np.array([3, 4])
result = a + b
print(result) # 輸出: [4 6]scalar = 3
vector = np.array([1, 2])
result = scalar * vector
print(result) # 輸出: [3 6]問:向量與標量的區別是什么?
問:如何計算一個二維向量的模?
問:單位向量有何應用?
問:如何在編程中實現向量的加法?
a + b。問:什么是零向量?
通過本文的詳盡解析,相信您對向量的基本概念、運算及其在數學與物理中的應用有了更加深刻的理解。