91精品一久久香蕉国产线看观看 ,久久99久久99精品免观看 ,精品一区二区三区免费

鄰接矩陣的定義與性質(zhì)

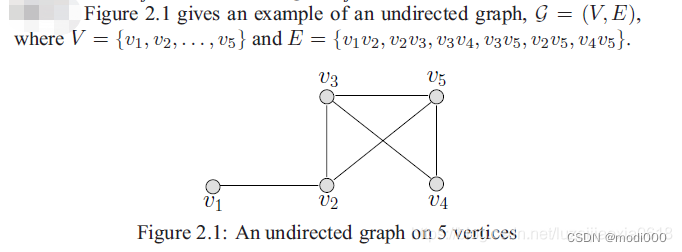
鄰接矩陣是圖論中的基本概念，用于表示圖中頂點(diǎn)之間的連接關(guān)系。對于一個圖G = (V, E)，其中V是頂點(diǎn)集，E是邊集，鄰接矩陣A是一個n階方陣（n為頂點(diǎn)數(shù)量），其元素A[i][j]表示頂點(diǎn)i到頂點(diǎn)j之間的邊關(guān)系。

無向圖的鄰接矩陣

無向圖的鄰接矩陣是對稱的，即A[i][j] = A[j][i]。
主對角線上的元素通常為零，表示無自環(huán)。

有向圖的鄰接矩陣

有向圖的鄰接矩陣不一定對稱。
A[i][j]表示從頂點(diǎn)i到頂點(diǎn)j的邊。

二階傳播的需求與挑戰(zhàn)

在圖神經(jīng)網(wǎng)絡(luò)中，二階傳播能夠捕獲更遠(yuǎn)距離的節(jié)點(diǎn)信息，提高模型的表達(dá)能力。然而，傳統(tǒng)的單層GNN架構(gòu)在進(jìn)行多階傳播時，容易導(dǎo)致節(jié)點(diǎn)特征過平滑的問題。為了解決這一問題，研究人員提出了多種改進(jìn)方案，包括引入正則化技術(shù)和優(yōu)化鄰接矩陣的使用方式。

二階傳播示例

二階傳播與節(jié)點(diǎn)特征

二階傳播可以通過鄰接矩陣的冪次操作實(shí)現(xiàn)。具體而言，鄰接矩陣A的k次冪A^k能夠表示節(jié)點(diǎn)之間的k跳關(guān)系。
通過累積不同階次的鄰接矩陣，可以實(shí)現(xiàn)多階特征的聚合。

鄰接矩陣在二階傳播中的作用

鄰接矩陣作為信息傳播的載體，直接影響著圖神經(jīng)網(wǎng)絡(luò)的表現(xiàn)。
在多階傳播中，鄰接矩陣的冪次操作能夠幫助模型捕獲更復(fù)雜的節(jié)點(diǎn)間關(guān)系。

Diffusion-Convolutional Neural Networks（DCNN）

DCNN是一種通過擴(kuò)散卷積實(shí)現(xiàn)多階傳播的圖神經(jīng)網(wǎng)絡(luò)模型。其核心思想是直接對每個節(jié)點(diǎn)采用多階跳的矩陣進(jìn)行表征，實(shí)現(xiàn)遠(yuǎn)程信息的聚合。

DCNN模型架構(gòu)

特征矩陣與鄰接矩陣：節(jié)點(diǎn)特征矩陣X與鄰接矩陣A結(jié)合，計(jì)算不同階次的轉(zhuǎn)移概率矩陣P。
多階聚合：通過累積不同階次的矩陣，計(jì)算每個節(jié)點(diǎn)的多跳鄰居信息。

class NodeClassificationDCNN(object):
    def __init__(self, parameters, A):
        self.params = parameters
        self.var_K = T.tensor3('Apow')
        self.var_X = T.matrix('X')
        self.var_Y = T.imatrix('Y')

    def get_output_for(self, inputs, **kwargs):
        Apow = inputs[0]
        X = inputs[1]
        Apow_dot_X = T.dot(Apow, X) # 公式中P與X的相乘
        Apow_dot_X_times_W = Apow_dot_X * self.W
        out = self.nonlinearity(Apow_dot_X_times_W)
        return out

Direct multi-hop Attention based GNN（DAGCN）

DAGCN通過在注意力機(jī)制中引入多跳信息，擴(kuò)展了GNN的感受野。其主要利用了Multi-hop Attention Diffusion操作，通過對多階次的注意力進(jìn)行加權(quán)，實(shí)現(xiàn)信息的更廣泛傳播。

DAGCN示例

DAGCN的多頭注意力機(jī)制

傳播注意力計(jì)算：利用LeakyReLU和tanh函數(shù)計(jì)算邊的傳播注意力。
注意力矩陣的定義：通過softmax函數(shù)規(guī)范化注意力得分。

多階傳播的效果

通過引入decay factor，DAGCN能夠有效控制多階傳播的影響范圍。
遠(yuǎn)處節(jié)點(diǎn)的attention weight會隨著傳播次數(shù)的增加而逐漸衰減。

圖論基礎(chǔ)：鄰接矩陣與度矩陣

在分析圖神經(jīng)網(wǎng)絡(luò)時，了解圖論基礎(chǔ)知識是至關(guān)重要的。鄰接矩陣和度矩陣是圖結(jié)構(gòu)數(shù)據(jù)的基本表示方式。

度矩陣的定義

度矩陣是一個對角矩陣，其對角元素表示圖中節(jié)點(diǎn)的度數(shù)。
在無向圖中，節(jié)點(diǎn)的度數(shù)為與該節(jié)點(diǎn)相連的邊的數(shù)量。

鄰接矩陣與度矩陣的關(guān)系

鄰接矩陣與度矩陣的乘積可以用于計(jì)算節(jié)點(diǎn)間的路徑數(shù)量。
在有向圖中，度矩陣分為出度矩陣和入度矩陣，分別表示節(jié)點(diǎn)的出邊和入邊數(shù)量。

度矩陣示例

鄰接矩陣的存儲與優(yōu)化

在大規(guī)模圖數(shù)據(jù)中，鄰接矩陣的存儲和計(jì)算開銷是一個重要的問題。為了提高計(jì)算效率，需要對鄰接矩陣進(jìn)行優(yōu)化。

稀疏矩陣存儲

由于大多數(shù)圖是稀疏的，鄰接矩陣的非零元素很少。
采用稀疏矩陣存儲可以有效減少存儲空間和計(jì)算量。

矩陣分解技術(shù)

對鄰接矩陣進(jìn)行分解，可以提高大規(guī)模圖數(shù)據(jù)的處理效率。
常用的分解技術(shù)包括LU分解、QR分解等。

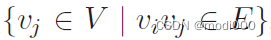
稀疏矩陣存儲示例

鄰接矩陣在實(shí)際應(yīng)用中的案例

鄰接矩陣在許多實(shí)際應(yīng)用中扮演著重要角色，尤其是在社交網(wǎng)絡(luò)、物流網(wǎng)絡(luò)等領(lǐng)域。

社交網(wǎng)絡(luò)分析

鄰接矩陣用于分析社交網(wǎng)絡(luò)中的用戶關(guān)系。
多階傳播可以幫助識別潛在的社交群體和影響力節(jié)點(diǎn)。

物流網(wǎng)絡(luò)優(yōu)化

鄰接矩陣用于表示物流網(wǎng)絡(luò)中的運(yùn)輸路線。
通過多階傳播，可以優(yōu)化運(yùn)輸路徑，提高物流效率。

結(jié)論

鄰接矩陣在多階傳播中的應(yīng)用為圖神經(jīng)網(wǎng)絡(luò)提供了強(qiáng)大的工具，能夠有效捕獲圖中節(jié)點(diǎn)間的復(fù)雜關(guān)系。通過對鄰接矩陣的優(yōu)化和模型的改進(jìn)，GNN在大規(guī)模圖數(shù)據(jù)中的應(yīng)用前景廣闊。

FAQ

問：什么是鄰接矩陣？
- 答：鄰接矩陣是一種用于表示圖中節(jié)點(diǎn)間關(guān)系的矩陣，其元素表示節(jié)點(diǎn)間是否存在邊連接。
問：多階傳播如何提高GNN的性能？
- 答：多階傳播允許信息在更大范圍內(nèi)傳播，能夠捕獲節(jié)點(diǎn)間更復(fù)雜的關(guān)系，從而提高模型的表達(dá)能力。
問：如何優(yōu)化鄰接矩陣的存儲？
- 答：可以通過稀疏矩陣存儲和矩陣分解技術(shù)來優(yōu)化鄰接矩陣的存儲和計(jì)算效率。
問：DCNN與傳統(tǒng)GNN有何不同？
- 答：DCNN通過擴(kuò)散卷積實(shí)現(xiàn)多階傳播，能夠在單層網(wǎng)絡(luò)中捕獲遠(yuǎn)程信息，而傳統(tǒng)GNN通常需要多層結(jié)構(gòu)。
問：鄰接矩陣在社交網(wǎng)絡(luò)分析中的作用是什么？
- 答：鄰接矩陣用于分析用戶關(guān)系，通過多階傳播可以幫助識別潛在的社交群體和影響力節(jié)點(diǎn)。